




Page suivante: 3.3 Cartographie basée sur les Niveau précédent: 3.2 Cartographie physique Page précédente: 3.2 Cartographie physique





Page suivante: 3.3 Cartographie basée sur les
Niveau précédent: 3.2 Cartographie physique
Page précédente: 3.2 Cartographie physique
Une carte de restriction identifie dans l'ADN une suite linéaire de sites séparés par une distance réelle (en nombre de paires de bases). Ces sites correspondent à des coupures de la séquence par des enzymes de restriction. Une enzyme de restriction est un outil biologique qui coupe, de manière reproductible, la molécule d'ADN en des sites correspondant à l'occurrence d'un motif de 4, 5 ou 6 bases spécifique à l'enzyme. On dit aussi que l'enzyme digère une séquence. Les tailles des fragments qui résultent de ces coupures sont ensuite mesurées. La cartographie de restriction a pour objectif de reconstituer la séquence d'ADN en réordonnant les fragments issus des digestions.
L'utilisation de modèles mathématiques pour constituer la carte de restriction s'appuie sur les résultats obtenus à partir de digestions partielles ou complètes de la séquence. En contrôlant les conditions expérimentales, on peut réaliser soit une digestion totale, soit une digestion partielle. En condition de digestion totale, tous les sites de coupure sont coupés, alors que dans une digestion partielle, une proportion des sites de coupures restent intacts.
On réalise généralement une digestion complète par enzyme et une double digestion qui consiste à utiliser simultanément deux enzymes (cf. Figure 5).
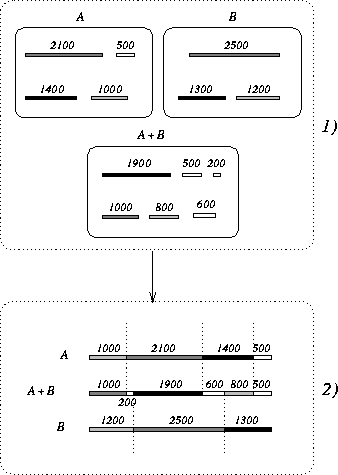
Figure 5: Illustration d'une double digestion complète. 1) La séquence
est digérée complètement par A en donnant 4 fragments, par B en
donnant 3 fragments puis par A+B en donnant 6 fragments. Le nombre de
permutations à analyser pour reconstruire la séquence à partir des deux
digestions simples est 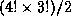 . Ainsi le nombre de cartes
possibles pour cet exemple est 72. 2) Reconstitution de la séquence.
Les fragments sont ordonnés de manière à satisfaire la reconstitution
simultanément pour la séquence coupée avec A, celle coupée avec B et
celle coupée avec A+B.
. Ainsi le nombre de cartes
possibles pour cet exemple est 72. 2) Reconstitution de la séquence.
Les fragments sont ordonnés de manière à satisfaire la reconstitution
simultanément pour la séquence coupée avec A, celle coupée avec B et
celle coupée avec A+B.
Le problème est alors de déduire la position des sites de coupure des enzymes de restriction à partir des longueurs des segments obtenus par l'action des enzymes A, B et A+B. En ignorant (très abusivement) d'éventuelles erreurs expérimentales, une instance du problème de la double digestion ou DDP est donc définie [ Lan 89] par :
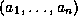 de longueurs produites par
l'action de l'enzyme A ;
de longueurs produites par
l'action de l'enzyme A ;
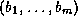 de longueurs produites par
l'action de l'enzyme B ;
de longueurs produites par
l'action de l'enzyme B ;
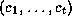 de longueurs produites par
l'action conjointe des enzymes A et B.
de longueurs produites par
l'action conjointe des enzymes A et B.
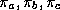 sur chacune des
listes de façon à ce que toute somme partielle
sur chacune des
listes de façon à ce que toute somme partielle
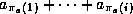 ou
ou 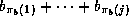 soit égale à une somme partielle
soit égale à une somme partielle  . La
permutation de la troisième liste découlant des deux premières, et à un
choix d'orientation près, le nombre de solutions potentielles est de l'ordre
de
. La
permutation de la troisième liste découlant des deux premières, et à un
choix d'orientation près, le nombre de solutions potentielles est de l'ordre
de 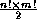 . Il faut noter qu'habituellement, il ne suffit
pas de trouver une solution, mais toutes les solutions.
. Il faut noter qu'habituellement, il ne suffit
pas de trouver une solution, mais toutes les solutions.
Cette formulation est extrêmement idéalisée car dans la pratique, du fait de la méthode expérimentale utilisée pour obtenir les longueurs :
 et il n'existe donc probablement pas
d'algorithme permettant de résoudre ce problème en temps polynomial dans le
pire des cas.
et il n'existe donc probablement pas
d'algorithme permettant de résoudre ce problème en temps polynomial dans le
pire des cas.
Dans la pratique, il est nécessaire d'énumérer exhaustivement les solutions et [ Gol 87] ont montré que, pour ce problème, le nombre de solutions croît en moyenne, et avec une probabilité de 1, de manière exponentielle en fonction de la longueur du segment d'ADN traité. Cependant, un nombre excessif de solutions est généralement sans intérêt et le problème doit être << contraint >> via l'utilisation d'autres sources d'informations (digestions partielles, autres enzymes...).
De nombreux programmes ont été développés pour répondre à ce problème [ Lan 89, Ing 94]. D'après [ Ing 94], il semble qu'une résolution basée sur la propagation de contraintes [ Ste 81] reste l'approche la plus robuste pour traiter simultanément digestions partielles et doubles digestions complètes. GA1 [ Ste 81] est un résolveur de problèmes sous contraintes dédié à la cartographie de restriction. Le problème peut se modéliser dans le cadre CSP de la façon suivante :
À chaque cycle, le résolveur de contraintes progresse en affectant une valeur soit à un site, soit à un fragment. Une affectation partielle inconsistante provoque un retour-arrière sur l'affectation précédente... Les principales qualités de GA1 relativement à d'autres approches sont sa robustesse quant au manque de fragments et son efficacité. Cette efficacité est associée à l'existence d'un nombre important d'heuristiques. De plus GA1 traite les digestions partielles et complètes contrairement à la plupart des programmes qui traitent uniquement des digestions complètes. Cependant, lorsque des erreurs se glissent dans les données (erreurs sur les longueurs de fragment par exemple) GA1 ne se comporte pas mieux (ni moins bien) que d'autres approches. En effet, pour des taux d'erreur réalistes sur les longueurs des fragments allant de 2,5% (minimum) à 10%, plusieurs milliers de cartes peuvent être générées. Ce nombre de solutions est bien trop élevé et revient à n'avoir aucune solution.
D'autres approches utilisent un résolveur de
contraintes [ All 88, Dix 88, Yap 93, Di 94].
[ All 88] tentent de prendre en compte les erreurs en
travaillant non plus sur des longueurs de fragments représentées par des
valeurs entières mais sur des intervalles. [ Di 94] utilisent le
langage de programmation logique avec contraintes CLP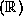 (les
techniques sous-jacentes sont issues de la programmation linéaire et non
des CSP). Les variables représentent le type d'enzyme ayant agi sur un site
et la localisation d'un site dans la séquence. Cette dernière approche
suppose que l'on dispose d'un jeu complet de fragments uniques de
restriction, qui à eux tous représentent la région entière à cartographier
ce qui est expérimentalement peu probable.
(les
techniques sous-jacentes sont issues de la programmation linéaire et non
des CSP). Les variables représentent le type d'enzyme ayant agi sur un site
et la localisation d'un site dans la séquence. Cette dernière approche
suppose que l'on dispose d'un jeu complet de fragments uniques de
restriction, qui à eux tous représentent la région entière à cartographier
ce qui est expérimentalement peu probable.





Page suivante: 3.3 Cartographie basée sur les
Niveau précédent: 3.2 Cartographie physique
Page précédente: 3.2 Cartographie physique
Copyright(C)1995
INRA
Tous droits réservés