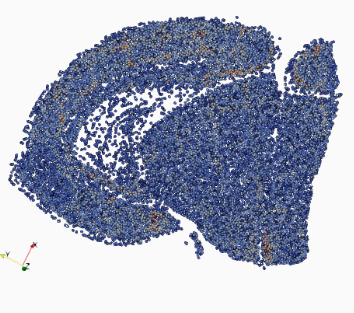
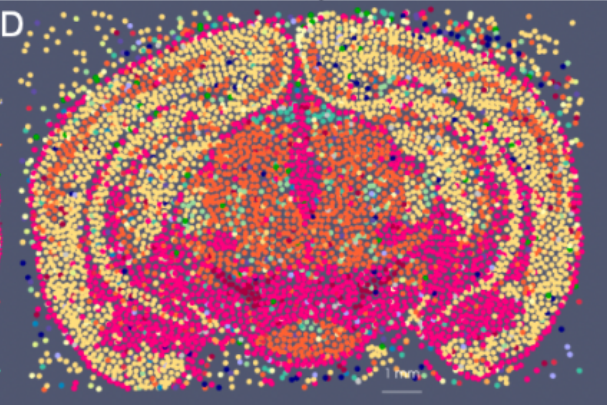
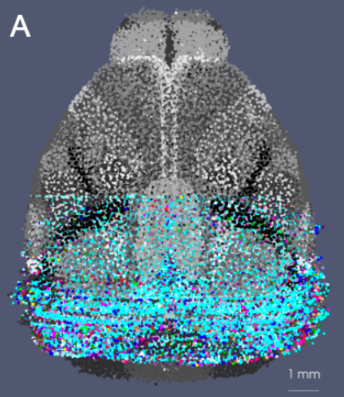
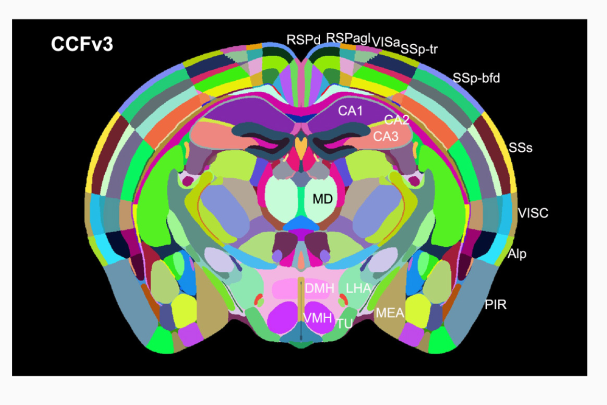
Representing and Mapping 3D Imaging and Spatial-omics Data Simultaneously Across Scales with Image-Varifold:
September 2025
Recent advances in imaging and molecular profiling technologies have enabled the acquisition of data at subcellular resolution. However, integrating such data across modalities, spatial scales, and ac...
quisition protocols remains a major challenge due to differences in resolution, feature types, and physical coverage. In this talk, I will present a suite of technologies we have developed for cross-modality 3D mapping, enabling non-rigid alignment of transcriptomic data at micron scales (genes and cells) to anatomical structures at tissue and organ scales. Our approach addresses three key challenges:- Comparing diverse modalities using the mathematical framework of image-varifold norms
- Managing massive data volumes through a multiscale strategy for computing non-rigid deformations efficiently
- Handling incomplete data via partial matching methods that map full-brain references to sparsely sampled sub-volumes
- Stouffer KM, Chen X, Zeng H, et al. xIV-LDDMM Toolkit: A Suite of Image-Varifold Based Technologies for Representing and Mapping 3D Imaging and Spatial-omics Data Simultaneously Across Scales. Nat Commun Biology. 2025. PubMed
- Stouffer KM, Trouvé A, Younès L, et al. Cross-modality mapping using image varifolds to align tissue-scale atlases to molecular-scale measures with application to 2D brain sections. Nat Commun. 2024 Apr 25;15(1):3530.PubMed
KeOps library: Scalable Kernel Methods [for Geometric Data]:
June 2025
In this talk I will present the KeOps library, which allows to compute arbitrary operations implying $M*N$ pairwise interactions between $M$ "source" and $N$ "target" data points or features in a very...
efficient way, benefitting from Cpu or Gpu parallelization and automatic differentiation. KeOps avoids creating unnecessary temporary quadratic matrices ($M \times N$) for very common operations such as kernel convolutions or nearest neighbour search and can be used almost seamlessly, through NumPy, PyTorch or R bindings. The end-user interface of KeOps is centered around the concept of symbolic matrices or tensors, i.e. tensors that are defined as mathematical expressions from actual tensors, are not computed nor materialized in memory, and can be further manipulated in expressions until the actual final computation is performed. KeOps allows to alleviate the user from the burden of creating custom routines for such operations, easing the development of algorithms for a broad range of applications in imaging science, such as inverse problems, computational optimal transport, shape analysis or geometric deep learning.No matching items