




Page suivante: 5 Planification d'expériences Niveau précédent: 4.2 Détermination de structures de Page précédente: 4.2.1 Détermination de structures de





Page suivante: 5 Planification d'expériences
Niveau précédent: 4.2 Détermination de structures de
Page précédente: 4.2.1 Détermination de structures de
Les structures 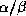 constituent une classe de structures parmi les
plus fréquentes et les plus régulières dans lesquelles les feuillets
constituent une classe de structures parmi les
plus fréquentes et les plus régulières dans lesquelles les feuillets 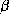 et les hélices
et les hélices  sont reliés par des régions dites ``en boucle'' de
longueur variable et de forme irrégulière. Dans la sous-classe des
structures en feuillets
sont reliés par des régions dites ``en boucle'' de
longueur variable et de forme irrégulière. Dans la sous-classe des
structures en feuillets 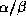 , les hélices sont situées de part et
d'autre du feuillet
, les hélices sont situées de part et
d'autre du feuillet 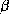 . Ces structures varient considérablement en
fonction de leur taille, du nombre et de l'ordre des brins
. Ces structures varient considérablement en
fonction de leur taille, du nombre et de l'ordre des brins 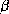 . À ce
propos, on peut souligner ici que les caractéristiques essentielles d'un
feuillet
. À ce
propos, on peut souligner ici que les caractéristiques essentielles d'un
feuillet 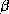 sont le nombre de brins
sont le nombre de brins 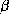 , leurs directions
relatives, parallèles ou anti-parallèles, et l'ordre dans lequel sont
connectés les brins dans la séquence polypeptidique.
, leurs directions
relatives, parallèles ou anti-parallèles, et l'ordre dans lequel sont
connectés les brins dans la séquence polypeptidique.
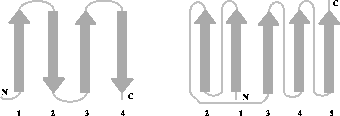
Figure 8: Les feuillets 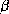 sont représentés par des flèches connectées
en une topologie mettant en évidence la direction de chaque brin
sont représentés par des flèches connectées
en une topologie mettant en évidence la direction de chaque brin 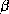 et l'enchaînement des brins
et l'enchaînement des brins 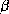 le long de la chaîne polypeptidique. A
gauche, 4 brins
le long de la chaîne polypeptidique. A
gauche, 4 brins 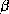 sont connectés en un feuillet
sont connectés en un feuillet 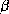 anti-parallèle. À droite, 5 brins
anti-parallèle. À droite, 5 brins 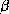 sont connectés en un feuillet
sont connectés en un feuillet
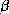 parallèle.
parallèle.
Pour la sous-classe des feuillets 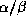 , quelques règles topologiques
connues permettent de dériver les topologies des structures secondaires
(hélices
, quelques règles topologiques
connues permettent de dériver les topologies des structures secondaires
(hélices  et feuillets
et feuillets 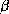 ). Sachant que la structure à
rechercher est un feuillet
). Sachant que la structure à
rechercher est un feuillet 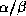 et connaissant les structures
secondaires, les auteurs ([ Cla 91]) s'appuient sur une
formalisation dans le cadre CSP afin de prédire les topologies en feuillets
et connaissant les structures
secondaires, les auteurs ([ Cla 91]) s'appuient sur une
formalisation dans le cadre CSP afin de prédire les topologies en feuillets
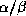 d'une protéine :
d'une protéine :
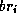 contenu dans le feuillet ;
la première variable,
contenu dans le feuillet ;
la première variable, 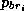 , représente la position du brin dans le
feuillet ; la deuxième variable,
, représente la position du brin dans le
feuillet ; la deuxième variable, 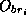 , donne l'orientation du brin
; la troisième variable est représentative de la nature de la connexion au
brin précédent ;
, donne l'orientation du brin
; la troisième variable est représentative de la nature de la connexion au
brin précédent ;
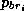 prend ses valeurs dans
l'intervalle
prend ses valeurs dans
l'intervalle 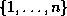 ; deux valeurs sont possibles pour la
deuxième variable : haut ou bas ; enfin, la troisième variable
peut prendre les valeurs droite ou gauche ; le nombre total de
topologies est alors, aux orientations près, de l'ordre de
; deux valeurs sont possibles pour la
deuxième variable : haut ou bas ; enfin, la troisième variable
peut prendre les valeurs droite ou gauche ; le nombre total de
topologies est alors, aux orientations près, de l'ordre de 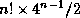 ;
;
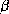 .
.
Une version parallélisée plus récente, ([ Cla 94]) permet de traiter l'incertitude au niveau des contraintes afin de résoudre des conflits potentiels entre données structurales et contraintes. L'introduction, dans la représentation d'une contrainte, de ses conditions de succès et d'échec assorties d'un poids (valeur entière positive) permet d'associer un coût (somme des pénalités correspondant aux contraintes non satisfaites) à chaque ensemble d'hypothèses topologiques. Ce coût est minimisé lors de la recherche par un algorithme de type Branch and Bound.





Page suivante: 5 Planification d'expériences
Niveau précédent: 4.2 Détermination de structures de
Page précédente: 4.2.1 Détermination de structures de
Copyright(C)1995
INRA
Tous droits réservés